10人がジャンケンでたった一人の勝者を決めるまでには,何回ジャンケンをするでしょうか。

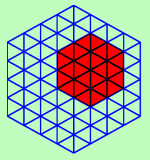
1辺の長さ4の正六角形(右図)の中に,正六角形はいくつ数えることができるでしょうか?
この問題は,私が高校生のときにZ会の添削問題として出題されたものです。私はとてもユニークな解答を考えたのですが,採点結果は0点でした。私の解答が不親切で採点者が理解できなかったのかも知れませんが,これがきっかけで私はZ会をやめました。
同じものが含まれる場合の円順列の総数を求めるのは非常に困難ですが,メビウス関数を用いた反転公式の利用で巧妙に求めることができます。
★改訂版が下記にあります。そちらをご覧ください。
いくつかのカードを並べ替えるとき,どのカードをとっても元の位置と異なる順列−完全順列−の個数を,階差数列に関する反転公式の利用で求めます。また,同じ手法を用いて,有限集合AからBへの全射の個数を求めます。
★改訂版が下記にあります。そちらをご覧ください。
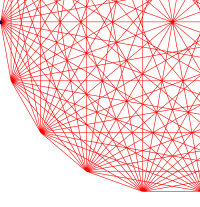
正18角形の対角線を引いてみると,多くの場所で4本以上の対角線が1点で交わっています(参照:正多角形の対角線)。これを,初等幾何と三角関数の2つの方法で調べてみました。
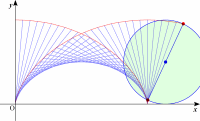
転がる円の円周上の1点の軌跡はサイクロイドですが,ひとつの直径が描く包絡線もまたサイクロイドです。これを易しく証明しました。
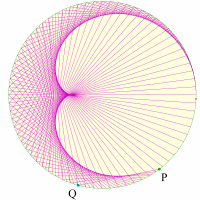
円周上を一定の速さで回る2点があり,これらは異なる速さで回っているとします。このとき,2点を結ぶ弦が描く包絡線は外サイクロイドになります。(参照:弦が描く模様)
これを上記の「転がる円の直径の包絡線」を利用して初等幾何学の知識で説明しました。
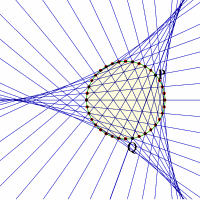
円周上を 1 : 2 の速さで逆方向に回転する2点を結ぶ直線が作る直線群の包絡線はデルトイド(内トロコイドのひとつ)ですが,ここでは,直線群の交点に注目してみると, 3本の直線が1点で交わっていることに気がつきます。
なぜ,1点で交わるのか。どのようなときに交わるのかを調べました。
円周上を 1 : 2 の速さで逆方向に回転する2点を結ぶ直線が作る直線群の諸性質を,複素平面上の方程式を用いて考察しました。直線群の包絡線がデルトイドであること,デルトイド内の点では直線群の直線が3本ずつ交わることなど,デルトイドの弦に関する多くの事柄が,簡潔な計算によって示されます。
コンピュータを利用していると,手作業では計算できない,あるいは描けないものを扱うことができるので,思わぬ発見に出会うことがある。とくに関数グラフツールGRAPESの場合,扱う対象が図形やグラフなので見ていてきれいな性質が多い。今回は,そのような発見※1の中から,内サイクロイドのひとつ―デルトイドに関する性質を紹介します。
このレポートは,2007年12月の大阪高等学校数学教育会の研究発表大会で話した内容を再編成したもので,でデルトイドの接線に関する性質に焦点をあてて,上記3つのレポート「転がる円の直径の包絡線」、「異なる速さで円周上を回る2点を結ぶ弦が作る模様」,「円周上を 1 : 2 の速さで逆方向に回る2点を結ぶ弦の交点について」をまとめた内容になっています。
このレポートは,関数グラフソフトGRAPES の定積分計算を改良する作業の中で見つけた積分公式です。4 次多項式による近似式を最適化することによって,9 次の多項式についても誤差を生まず,かつ,それ以上の次数の項についても誤差の非常に小さい積分の近似式を得ることができました。
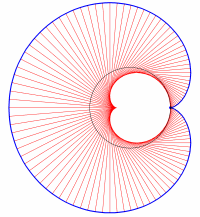
サイクロイドの縮閉線はこれと合同なサイクロイドであり,外(内)サイクロイドの縮閉線はこれと相似な外(内)サイクロイドである。これを,微積分を用いずに極めて簡潔に説明します。さらにこの結果を用いて,サイクロイドの弧長を求めます。
数列と高次階差数列との間には,「二項係数の反転公式」と呼ばれる,裏返しの関係があります。
約数についての総和に関しては,「メビウスの反転公式」と呼ばれる反転公式があります。
また,和集合の要素の個数に関しても,補集合を考えることにより,反転公式と類似の関係
を見出すことができます。
第1節では,完全順列の総数や全射の総数について,二項係数の反転公式を利用した求め方を述べます。
第2節では,任意の円順列の総数の求め方を述べます。同じものが含まれる円順列では,多くの場合,その総数の導出が非常に困難です。これを,メビウスの反転公式を利用して導出します。
第3節では,集合の要素の個数に関する公式を導き,それを利用して,完全順列の総数や全射の総数を導出します。また,円順列の総数についても,再び触れます。