領域内の格子点
サンプルに，陽関数のグラフで「格子点強調」というものが
ありましたが，不等式の表す領域内に存在する格子点を表示
することは可能でしょうか。
(x^2+y^2<=20)and((x-int(x+.5))^2+(y-int(y+.5))^2<.003)
ってしてみましたけど，うまくいきませんでした。
ありましたが，不等式の表す領域内に存在する格子点を表示
することは可能でしょうか。
(x^2+y^2<=20)and((x-int(x+.5))^2+(y-int(y+.5))^2<.003)
ってしてみましたけど，うまくいきませんでした。
[添付]: 4986 bytes
Quasi
お願い
テザルグの定理の画面が欲しい
Re: お願い
ともだ 
2015/02/17(Tue) 07:52 No.2092
サンプルの幾何フォルダに入っています。
ともだ 2015/02/17(Tue) 07:52 No.2092
バレンタインデー
色々なハート関数を考える人が居られます。
まずは、３Dです。
まずは、３Dです。
[添付]: 1793 bytes
楕円上の点の動き
いつもお世話になりもうしわけありません。
教えてください。
楕円, 4x^2+9y^2=36 上の点P を
P(t,√(36-4t^2/3))として入力して動かして
います。楕円の上半分だけは動かせますが。
そのことは十分に分かっておりますが,
点pを楕円上を一周させる方法が分かりません。
ご指導くださいませ。
高田大進吉
教えてください。
楕円, 4x^2+9y^2=36 上の点P を
P(t,√(36-4t^2/3))として入力して動かして
います。楕円の上半分だけは動かせますが。
そのことは十分に分かっておりますが,
点pを楕円上を一周させる方法が分かりません。
ご指導くださいませ。
高田大進吉
Re: 楕円上の点の動き
ともだ 2015/02/08(Sun) 13:48 No.2084
楕円の方程式を，標準形 x^2/a^2 + y^2/b^2 = 1 で表したとき，
この楕円上の点は，(a cos t , b sin t )で表されます。
> 楕円, 4x^2+9y^2=36 上の点P を
この場合は，a = 3 , b = 2 です。
この楕円上の点は，(a cos t , b sin t )で表されます。
> 楕円, 4x^2+9y^2=36 上の点P を
この場合は，a = 3 , b = 2 です。
ともだ 2015/02/08(Sun) 13:48 No.2084
Re: 楕円上の点の動き
できました。
ありがとうございました。
高田大進吉
ありがとうございました。
高田大進吉
楕円の焦点表示
お世話になります。
中学段階の表示はほぼパワーポイント上に掲載
しながら表現可能となりました。
ご指導ありがとうございます。
これから高校範囲に指導に活用して, と思っております。
１ 楕円の焦点の表示はスクリプトにどのように入力すれば
いいのでしょうか。
ご指導よろしくお願いいたします。
高田大進吉
中学段階の表示はほぼパワーポイント上に掲載
しながら表現可能となりました。
ご指導ありがとうございます。
これから高校範囲に指導に活用して, と思っております。
１ 楕円の焦点の表示はスクリプトにどのように入力すれば
いいのでしょうか。
ご指導よろしくお願いいたします。
高田大進吉
Re: 楕円の焦点表示
ともだ 2015/01/29(Thu) 08:36 No.2079
楕円の方程式がわかっているのでしたら，焦点の座標を持つ点を作ればよいだけかと思いますが・・・
スクリプトで何をされたいのでしょうか？
スクリプトで何をされたいのでしょうか？
ともだ 2015/01/29(Thu) 08:36 No.2079
Re: 楕円の焦点表示
円の場合, C+aroll(@) で中心 C で半径 a の円を
簡便に表示できました。
このような楕円の簡便な表示があるのかなあ,と思いました。
楕円の場合は焦点から楕円を表示するのかなあ,と思いました。楕円に 焦点の中点 C を認めるならば, そこから楕円
表示は可能かなあ,と思いました。
簡便に表示できました。
このような楕円の簡便な表示があるのかなあ,と思いました。
楕円の場合は焦点から楕円を表示するのかなあ,と思いました。楕円に 焦点の中点 C を認めるならば, そこから楕円
表示は可能かなあ,と思いました。
Re: 楕円の焦点表示
ともだ 2015/01/30(Fri) 21:40 No.2081
GRAPESについての技術的な質問にはお答えしますが、これは数学の内容です。ご自分でお調べください。
高校３年の教科書には出ていると思いますが。
高校３年の教科書には出ていると思いますが。
ともだ 2015/01/30(Fri) 21:40 No.2081
Re: 楕円の焦点表示
友田 先生
分かりました。
調べてみます。ありがとうございました。
分かりました。
調べてみます。ありがとうございました。
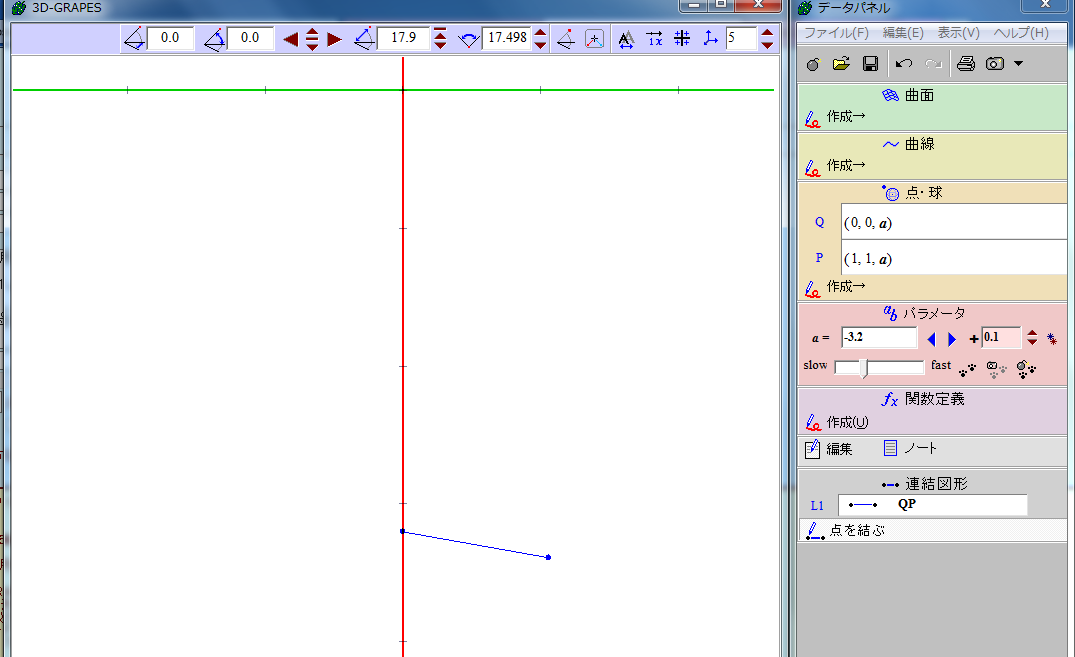
バグ？
3D-GRAPES 1.70を使用しています。
点P(0,0,a)と点Q(1,1,a)を結び、パラメータaを動かします。
これをyz平面で見たとき、線分PQはy軸に平行でなければなりませんが、明らかに平行になっていません。
バグでしょうか？
※ちなみに、点Qを(0,1,a)にして同様のことをすると正しく平行に表示されます。
点P(0,0,a)と点Q(1,1,a)を結び、パラメータaを動かします。
これをyz平面で見たとき、線分PQはy軸に平行でなければなりませんが、明らかに平行になっていません。
バグでしょうか？
※ちなみに、点Qを(0,1,a)にして同様のことをすると正しく平行に表示されます。
Re: バグ？
ともだ 2015/01/22(Thu) 16:56 No.2073
点Pと点Qでは，視点からの距離が異なるために，遠近法の設定によって，平行には見えないのです。
3D-GRAPESは遠近法に従って描画しています。
そのため近くのものは大きく，遠くのものは小さく表示されます。
ご指摘の線分PQをy軸と平行に見せるには，無限遠のかなたから見るしかありません。
そのためには，平行投影ボタンを利用します。
（PDFマニュアルの「視点の移動とズーミング」を参照のこと）
3D-GRAPESは遠近法に従って描画しています。
そのため近くのものは大きく，遠くのものは小さく表示されます。
ご指摘の線分PQをy軸と平行に見せるには，無限遠のかなたから見るしかありません。
そのためには，平行投影ボタンを利用します。
（PDFマニュアルの「視点の移動とズーミング」を参照のこと）
ともだ 2015/01/22(Thu) 16:56 No.2073
Re: バグ？
クロキ 2015/01/22(Thu) 17:07 No.2074
ありがとうございます。
あともう一点質問させてください。
yz平面を表示し、視野角の数値をいじると、不正な不動小数点数演算命令というエラーが出るのですが、これも遠近法と関連があるのでしょうか？
あともう一点質問させてください。
yz平面を表示し、視野角の数値をいじると、不正な不動小数点数演算命令というエラーが出るのですが、これも遠近法と関連があるのでしょうか？
クロキ 2015/01/22(Thu) 17:07 No.2074
Re: バグ？
ともだ 2015/01/22(Thu) 17:22 No.2075
>不正な不動小数点数演算命令というエラーが出るのですが、
こちらでも再現しています。
今から調べます。
こちらでも再現しています。
今から調べます。
ともだ 2015/01/22(Thu) 17:22 No.2075
Re: バグ？
ともだ 2015/01/22(Thu) 18:11 No.2076
新しく書き換えた部分のバグでした。
先ほど修正したものを同じファイル名でUPしました。
このバグに関するコメントは何も表示していませんが，ファイルは新しくなっています。
DownLoadして試してください。
先ほど修正したものを同じファイル名でUPしました。
このバグに関するコメントは何も表示していませんが，ファイルは新しくなっています。
DownLoadして試してください。
ともだ 2015/01/22(Thu) 18:11 No.2076
Re: バグ？
クロキ 2015/01/23(Fri) 10:49 No.2077
丁寧な御回答ありがとうございました。
試してみます。
試してみます。
クロキ 2015/01/23(Fri) 10:49 No.2077