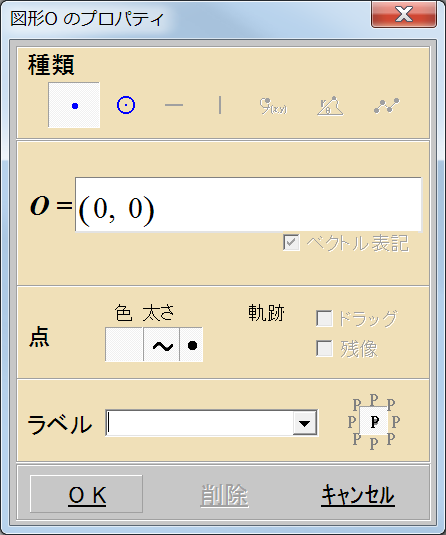
目盛りの設定
初めまして。
ワードでプリントを作る際にグラフを書くには…と検索して、ここにたどり着きました。
非常に高性能で助かっております。
１つ質問させて下さい。目盛りを対数目盛にして、対数グラフを直線で見たいのですが、それは可能でしょうか？
ワードでプリントを作る際にグラフを書くには…と検索して、ここにたどり着きました。
非常に高性能で助かっております。
１つ質問させて下さい。目盛りを対数目盛にして、対数グラフを直線で見たいのですが、それは可能でしょうか？
Re: 目盛りの設定
ともだ 
2015/11/10(Tue) 15:05 No.2201
対数目盛には対応していません。
ともだ 2015/11/10(Tue) 15:05 No.2201
離心率と２次曲線（陰関数）
極方程式で表された２次曲線の、離心率による変化を
見ようとして、陰関数表示で
ｒ＝as/（1＋ｓcosθ）
としたところ、ｓ＞1ではうまくいきません。
これは、陰関数表示ではむずかしいのでしょうね・・・。
曲線表示のほうでは大丈夫です。
見ようとして、陰関数表示で
ｒ＝as/（1＋ｓcosθ）
としたところ、ｓ＞1ではうまくいきません。
これは、陰関数表示ではむずかしいのでしょうね・・・。
曲線表示のほうでは大丈夫です。
[添付]: 4846 bytes
Re: 離心率と２次曲線（陰関数）
ともだ 2015/10/28(Wed) 18:38 No.2195
陰関数は連続な関数にしか対応していません。
s>1のとき，不連続点が生じます。
s>1のとき，不連続点が生じます。
ともだ 2015/10/28(Wed) 18:38 No.2195
Re: 離心率と２次曲線（陰関数）
ともだ 2015/10/28(Wed) 19:33 No.2196
追伸です。
C1: r(1+scosθ)=as
とすれば両辺は連続関数になるので，正しく描画されます。
ただし，陰関数の中では，
r≧0 ,0≦θ<2π
という制約があるので，双曲線は片方しか描画されません。
もう一方を描くには，
C2: -r(1+scos(θ+π))=as
とでもすることになります。
C1: r(1+scosθ)=as
とすれば両辺は連続関数になるので，正しく描画されます。
ただし，陰関数の中では，
r≧0 ,0≦θ<2π
という制約があるので，双曲線は片方しか描画されません。
もう一方を描くには，
C2: -r(1+scos(θ+π))=as
とでもすることになります。
[添付]: 4932 bytes
ともだ 2015/10/28(Wed) 19:33 No.2196
Re: 離心率と２次曲線（陰関数）
北摂三太郎 2015/10/29(Thu) 07:45 No.2197
早速のご返答ありがとうございます。すっきりしました。
北摂三太郎 2015/10/29(Thu) 07:45 No.2197
階段状の点列の極限
こんにちは。いつも利用させていただき，ありがとうございます。
数IIIで，点列の極限
P_0は原点，P_1は(1,0)
P_{n+1}P_{n+2}=1/2 P_{n}P_{n+1}
かつ角P_{n}P_{n+1}P_{n+2}=Pi/2
を指導する際に，
渦巻き状に進む場合は複素数が有効だと思ってファイルを
作ったのですが，階段状の場合はうまい考えが浮かびません
でした。
何か妙案はありますか。
数IIIで，点列の極限
P_0は原点，P_1は(1,0)
P_{n+1}P_{n+2}=1/2 P_{n}P_{n+1}
かつ角P_{n}P_{n+1}P_{n+2}=Pi/2
を指導する際に，
渦巻き状に進む場合は複素数が有効だと思ってファイルを
作ったのですが，階段状の場合はうまい考えが浮かびません
でした。
何か妙案はありますか。
[添付]: 5838 bytes
領域内の格子点
Quasi 2015/10/24(Sat) 20:00 No.2191
ぶちゃいくな階段状のヤツです
[添付]: 5548 bytes
Quasi 2015/10/24(Sat) 20:00 No.2191
Re: 階段状の点列の極限
ともだ 2015/10/24(Sat) 21:27 No.2192
渦巻き対応のものですが，複素数の演算とスクリプトを使って作ってみました。
階段状のものって，この漸化式から出ないように思いますが・・・
∠ABCと∠CBAでは符号が違うのではないでしょうか。
> 角P_{n}P_{n+1}P_{n+2}=Pi/2
この条件では，左回りか右回りになりませんか。
階段状のものって，この漸化式から出ないように思いますが・・・
∠ABCと∠CBAでは符号が違うのではないでしょうか。
> 角P_{n}P_{n+1}P_{n+2}=Pi/2
この条件では，左回りか右回りになりませんか。
[添付]: 5910 bytes
ともだ 2015/10/24(Sat) 21:27 No.2192
Re: 階段状の点列の極限
Quasi 2015/10/24(Sat) 23:00 No.2193
そうですね。漸化式ではあきませんね。失礼しました。
進行方向に対して左->右->左->右と進む階段状のもの，
と捉えてください。
進行方向に対して左->右->左->右と進む階段状のもの，
と捉えてください。
Quasi 2015/10/24(Sat) 23:00 No.2193
定義域のある関数の値域について
タイトルの件の説明をしようと添付したファイルを作りました。
x>-1のときの説明をしたいので，とりあえずtを大きくしようとt=50とするとQの範囲がおかしくなります。
表示領域をもっと広域にすると表示は正しくなります。
どこか変数の設定を間違えているのでしょうか。
おろしくお願いします。
x>-1のときの説明をしたいので，とりあえずtを大きくしようとt=50とするとQの範囲がおかしくなります。
表示領域をもっと広域にすると表示は正しくなります。
どこか変数の設定を間違えているのでしょうか。
おろしくお願いします。
[添付]: 5042 bytes
Re: 定義域のある関数の値域について
ともだ 2015/10/17(Sat) 10:55 No.2181
手元では，異常は再現しませんでした。
よろしければ，どのような異常が生じたのかを具体的にお教えいただけませんでしょうか。
よろしければ，どのような異常が生じたのかを具体的にお教えいただけませんでしょうか。
ともだ 2015/10/17(Sat) 10:55 No.2181
Re: 定義域のある関数の値域について
tanak 2015/10/18(Sun) 19:23 No.2184
t=50とすると表示領域がすべて赤くなります。
拡大縮小で-12<=x<=12ぐらいを表示させると正しくy<1の範囲が赤く表示されます。
ver7.13です。
拡大縮小で-12<=x<=12ぐらいを表示させると正しくy<1の範囲が赤く表示されます。
ver7.13です。
tanak 2015/10/18(Sun) 19:23 No.2184
Re: 定義域のある関数の値域について
ともだ 2015/10/18(Sun) 21:05 No.2185
不具合の状況はわかりましたが，手元のwin7,win10 の２台では確認できませんでした。手元で異常が生じないことには，すぐには対処できません。ご了解ください。
なお，点（水平線）Ｑの定義はもっと簡単に書くことができます。サンプルを添付します。
なお，点（水平線）Ｑの定義はもっと簡単に書くことができます。サンプルを添付します。
[添付]: 4982 bytes
ともだ 2015/10/18(Sun) 21:05 No.2185
Re: 定義域のある関数の値域について
ともだ 2015/10/18(Sun) 22:25 No.2186
追伸です。
手元のSurfacePro3(win10)で異常が出ました。
これで作業がはかどります。
ただし，OSに依存する症状かも知れないので，対策にhあ手間取る可能性があります。
手元のSurfacePro3(win10)で異常が出ました。
これで作業がはかどります。
ただし，OSに依存する症状かも知れないので，対策にhあ手間取る可能性があります。
ともだ 2015/10/18(Sun) 22:25 No.2186
Re: 定義域のある関数の値域について
tanak 2015/10/19(Mon) 11:08 No.2187
t=40までは正常ですが，t=41とするとy>2.2くらいが，t=42とするとy>5.2くらいが，t=43とするとすべてが赤くなります。
また，t=41として上にスクロールするとy軸の表示範囲は変わりますが，赤くなる範囲は変わりません。ほぼ画面の下半分が赤くなります。またt=42のときも同様で画面の下3/4くらいが赤くなります。
また，t=41として上にスクロールするとy軸の表示範囲は変わりますが，赤くなる範囲は変わりません。ほぼ画面の下半分が赤くなります。またt=42のときも同様で画面の下3/4くらいが赤くなります。
tanak 2015/10/19(Mon) 11:08 No.2187
Re: 定義域のある関数の値域について
tanak 2015/10/19(Mon) 21:53 No.2188
連絡が遅れましたが，私はwin7です。
tanak 2015/10/19(Mon) 21:53 No.2188
Re: 定義域のある関数の値域について
ともだ 2015/10/19(Mon) 22:28 No.2189
詳細な報告を頂きありがとうございました。
おかげで，原因をほぼ特定するときができました。
現在，対策を考えているところです。
近いうちに修正版を出すことができると思います。
おかげで，原因をほぼ特定するときができました。
現在，対策を考えているところです。
近いうちに修正版を出すことができると思います。
ともだ 2015/10/19(Mon) 22:28 No.2189
y=tan(x)のグラフの描画について
既出の質問であれば、申し訳ないです。
xがπ/4を含む区間、例えば[0,π/2]でy=tan(x)のグラフを
描画する場合、xがπ/4の近傍である場合のグラフ描画のアルゴリズムには特殊なものがあると聞きます。
その内容についての助言や参考文献の例示等をして頂ければ幸いです。
xがπ/4を含む区間、例えば[0,π/2]でy=tan(x)のグラフを
描画する場合、xがπ/4の近傍である場合のグラフ描画のアルゴリズムには特殊なものがあると聞きます。
その内容についての助言や参考文献の例示等をして頂ければ幸いです。
Re: y=tan(x)のグラフの描画について
ともだ 2015/10/18(Sun) 10:06 No.2183
tan(x) に関しては，GRAPESの開発環境であるDelphiのライブラリを利用しています。
ともだ 2015/10/18(Sun) 10:06 No.2183
不等式の領域が上手く表示されない
数年前の新潟の数学全国大会でご挨拶させていただいたことのある、岡山の高校教員の江川と申します。いつもGRAPESにはお世話になっています。
連立不等式の領域で
x^2 +y^2 <25and3x-y+3<0 は上手く表示されます。
しかし
(x-5)^2 +(y-5)^2 <25andx+2y-10>0 ga
表示されません。（直線になります）
前後を入れ換えて
x+2y-10>0and(x-5)^2 +(y-5)^2 <25 と入力すると
上手く表示されます。
なにか法則があるのでしょうか。
よろしくお願いいたします。
連立不等式の領域で
x^2 +y^2 <25and3x-y+3<0 は上手く表示されます。
しかし
(x-5)^2 +(y-5)^2 <25andx+2y-10>0 ga
表示されません。（直線になります）
前後を入れ換えて
x+2y-10>0and(x-5)^2 +(y-5)^2 <25 と入力すると
上手く表示されます。
なにか法則があるのでしょうか。
よろしくお願いいたします。
Re: 不等式の領域が上手く表示されない
ともだ 2015/10/16(Fri) 21:36 No.2179
複数の領域の共通部分や和集合を表示させるときには，
それそれの不等式を（）で囲んでください。
(x^2 +y^2 <25) and (3x-y+3<0)
あるいは
((x-5)^2 +(y-5)^2 <25) and (x+2y-10>0)
GRAPES内での処理の都合上，このような仕様になっています。
（PDFマニュアルの「4-3 複数の領域の共通部分と和集合」）
それそれの不等式を（）で囲んでください。
(x^2 +y^2 <25) and (3x-y+3<0)
あるいは
((x-5)^2 +(y-5)^2 <25) and (x+2y-10>0)
GRAPES内での処理の都合上，このような仕様になっています。
（PDFマニュアルの「4-3 複数の領域の共通部分と和集合」）
ともだ 2015/10/16(Fri) 21:36 No.2179
質問です
grapesは、windows10でも動きますか？
また、grapes 3Dを起動するためのOSはなんですか？
また、grapes 3Dを起動するためのOSはなんですか？
Re: 質問です
ともだ 2015/09/29(Tue) 18:54 No.2177
grapesはwin10でも動きます。
3Dに関しては，一応動いていますが，きちんと確認したわけではありません。確実に動くのは windows Vista/7/8/8.1 です。XPは動くと思いますが，動作確認をしていません。
3Dに関しては，一応動いていますが，きちんと確認したわけではありません。確実に動くのは windows Vista/7/8/8.1 です。XPは動くと思いますが，動作確認をしていません。
ともだ 2015/09/29(Tue) 18:54 No.2177
交線
円筒 x^2 + y^2 = 1 と 平面; -y + z = 0 との 交線は楕円であることを示し, その面積を求めよ
円筒 x^2 + y^2 = 1 と 平面;1*z + 2*y + 3 z + 4 = 0 との 交線は楕円であることを示し, その面積を求めよ
円筒 x^2 + y^2 = 1 と 平面;1*z + 2*y + 3 z + 4 = 0 との 交線は楕円であることを示し, その面積を求めよ
Re: 交線
ともだ 2015/09/25(Fri) 23:51 No.2175
その問題がどうしたのですか？
ともだ 2015/09/25(Fri) 23:51 No.2175
原点０の非表示（削除）方法
はじめまして。自宅で中学生と１対１で勉強しています。
最近こちらのソフトを使いはじめたばかりの素人です。
座標平面で軸のｘ、ｙの文字と同じように、原点０の表示を消すことはできますか？表示位置を変えたいときがあります。
ありましたら、その方法を教えてください。
最近こちらのソフトを使いはじめたばかりの素人です。
座標平面で軸のｘ、ｙの文字と同じように、原点０の表示を消すことはできますか？表示位置を変えたいときがあります。
ありましたら、その方法を教えてください。
Re: 原点０の非表示（削除）方法
ともだ 2015/09/15(Tue) 23:10 No.2172
原点の位置で右クリックして，［基本図形のプロパティ］をクリック
表示したいラベルの位置を選びます。
ラベルを消すには，ラベル「Ｏ」を削除して空欄にし，ラベル表示位置をどれか一つクリックします。（添付の図）
表示したいラベルの位置を選びます。
ラベルを消すには，ラベル「Ｏ」を削除して空欄にし，ラベル表示位置をどれか一つクリックします。（添付の図）
ともだ 2015/09/15(Tue) 23:10 No.2172
Re: 原点０の非表示（削除）方法
分かってしまえば・・・という感じです。
早々のレスポンス、ありがとうございました。
早々のレスポンス、ありがとうございました。
コラッツ予想について
数学素人なのでで稚拙で読みづらく間違いも多いと思いまして大変恐縮なのですが、標記について私なりの考えをURLに纏めてみましたので、よろしくご査収の上御高評賜れば幸いです。
Re: コラッツ予想について
ともだ 2015/09/12(Sat) 14:31 No.2170
貴重な証明をお知らせいただきありがとうございます。
ただ，ここしばらくの間じっくりと証明を読む余裕がありません。申し訳ありませんが，他の方をあたってもらえませんでしょうか。
ただ，ここしばらくの間じっくりと証明を読む余裕がありません。申し訳ありませんが，他の方をあたってもらえませんでしょうか。
ともだ 2015/09/12(Sat) 14:31 No.2170