3D-GRAPESのサンプルの円錐曲線について
サンプルの円錐曲線では双曲線が一つしか表示されないので，上半分を付け加えたいと思っています。
曲面Qで上側を表示させたいと思い，mcoss+n>0の条件を変えればよいのではないかと思ったのですが，残念ながら力不足でわかりません。何かよい方法があれば教えください。
よろしくお願いします。
曲面Qで上側を表示させたいと思い，mcoss+n>0の条件を変えればよいのではないかと思ったのですが，残念ながら力不足でわかりません。何かよい方法があれば教えください。
よろしくお願いします。
[添付]: 2555 bytes
tanak
点の結び方
点A（１，２）への返信ありがとうございます。
また初心者の質問で申し訳ありません。
もう一つ質問お願いします。
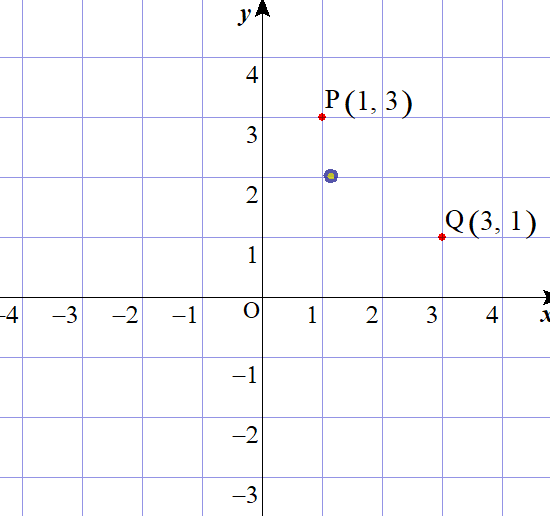
点P(1,３)と点Q（３，１）を表示させた後、
この2点を線分で結ぶ方法を教えてください。
最初の画面で、最下段の「点を結ぶ」をクリックすると
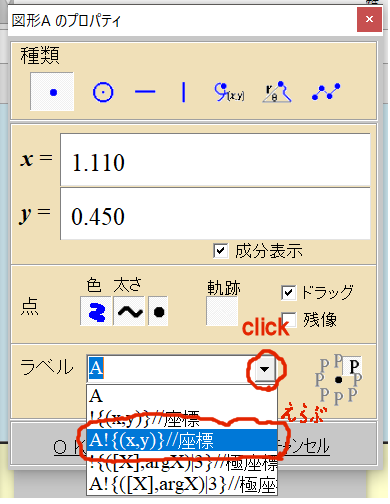
一番上に頂点の欄とBSがありますが、これは何でしょうか。
添付ファイルのように最初に座標が表示されているとき、ラベル欄はどう使うのでしょうか。また残像とは何でしょうか。
どうぞよろしくお願いいたします。
また初心者の質問で申し訳ありません。
もう一つ質問お願いします。
点P(1,３)と点Q（３，１）を表示させた後、
この2点を線分で結ぶ方法を教えてください。
最初の画面で、最下段の「点を結ぶ」をクリックすると
一番上に頂点の欄とBSがありますが、これは何でしょうか。
添付ファイルのように最初に座標が表示されているとき、ラベル欄はどう使うのでしょうか。また残像とは何でしょうか。
どうぞよろしくお願いいたします。
Re: 点の結び方
まず，マニュアルを読んでください。
［ヘルプ］メニューに［PDFマニュアル］があるので，クリックするとマニュアルが開きます。
点を結んだ図形に関することは，「連結図形」の章にあります。
なお「BS」は選んだ頂点を修正するためのもので，通常，最後に選んだ点が削除されます。
残像については，要するに，動いた後に残した図形のことですが，第5章「点と軌跡」に説明があります。
マニュアルに書いてないことや，わからなかったことを質問されるようお願いします。
［ヘルプ］メニューに［PDFマニュアル］があるので，クリックするとマニュアルが開きます。
点を結んだ図形に関することは，「連結図形」の章にあります。
なお「BS」は選んだ頂点を修正するためのもので，通常，最後に選んだ点が削除されます。
残像については，要するに，動いた後に残した図形のことですが，第5章「点と軌跡」に説明があります。
マニュアルに書いてないことや，わからなかったことを質問されるようお願いします。
座標
グラフ上に以下のように座標も表示する方法を教えてください
A（１，２）
A（１，２）
Re: 座標
図形Ａのプロパティ画面で，ラベル欄右端の▼をクリックし
「A!{(x,y)}//座標」を選びます。
「A!{(x,y)}//座標」を選びます。
7/16に質問をした者です
ソフトの操作方法が間違っているのか、問題に対する考え方が間違っているのか、その両方が間違っているのか、よく分からなくなってしまったので質問することにします。
以下の問題のグラフを描きたいと思っていますが、上手く書けませんでした。
当たりくじ赤が出る確率は常にaで一定、
当たりくじ青が出る確率は常にbで一定、
ハズレくじが出る確率は常に(1-a-b)で一定、
今は、a=bであると仮定します。
この条件下で、くじをn回引いたとき、
少なくとも５回以上当たりくじ赤が出て、かつ、少なくとも５回以上当たりくじ青が出る確率Pn(10≦n)を、
nの値に応じて確率が変化する様子をグラフで描く
という問題を考えています。
(これよりもさらに複雑な条件の問題を考えていますが、まずはこの問題が解けないとどうしようもないので。)
以下、自分が考えた解法です。
(赤が出る回数が0回、青が出る回数が0～n回いずれかになる確率)=A0
(赤が出る回数が1回、青が出る回数が0～n-1回いずれかになる確率)=A1
(赤が出る回数が2回、青が出る回数が0～n-2回いずれかになる確率)=A2
(赤が出る回数が3回、青が出る回数が0～n-3回いずれかになる確率)=A3
(赤が出る回数が4回、青が出る回数が0～n-4回いずれかになる確率)=A4
A=A0+A1+A2+A3+A4、と定義
(赤が出る回数が0～n回いずれか、青が出る回数が0回になる確率)=B0
(赤が出る回数が0～n-1回いずれか、青が出る回数が1回になる確率)=B1
(赤が出る回数が0～n-2回いずれか、青が出る回数が2回になる確率)=B2
(赤が出る回数が0～n-3回いずれか、青が出る回数が3回になる確率)=B3
(赤が出る回数が0～n-4回いずれか、青が出る回数が4回になる確率)=B4
B=B0+B1+B2+B3+B4、と定義
(赤が出る回数が0回、青が出る回数が0～4回いずれかになる確率)=C0
(赤が出る回数が1回、青が出る回数が0～4回いずれかになる確率)=C1
(赤が出る回数が2回、青が出る回数が0～4回いずれかになる確率)=C2
(赤が出る回数が3回、青が出る回数が0～4回いずれかになる確率)=C3
(赤が出る回数が4回、青が出る回数が0～4回いずれかになる確率)=C4
C=C0+C1+C2+C3+C4、と定義
ここで、a=bより、A=Bであるから
求める確率Pnは、
Pn=1-(A+B)+C
=1-2A+C
になると思ったので、AとCを計算しようと思い
まずは確率C=C0+C1+C2+C3+C4を計算しようと思いました。
ソフトでの表記方法に従うと、例えばC3の場合、
C3=(n,Sum(t,0,4,n!/3!t!(n-t-3)!×a^3×b^t×(1-a-b)^(n-t-3))
だと思ったので、
Cの場合だと、
C=(n,Sum(s,0,4,Sum(t,0,4,n!/s!t!(n-s-t)!×a^s×b^t×(1-a-b)^(n-s-t)))
次にAは
A=Sum(u,0,4,a^u×(1-a)^(n-u)×nCr(n,u))
になると思いました。
ここで、Pn=1-2A+C
のPnをグラフを描こうと思い、
パラメータを例えば、a=b=0.02の場合と仮定して、これをグラフにしたところ、
かなり早い段階でグラフが途切れてしまいました。
pdfでの説明の通りに、(変域の上端ー下端)/増減幅≦5000の範囲にしてるのですが、なぜこんなに早くグラフが途切れるのでしょうか。
この問題では、どう入力するのが正しかったのでしょうか。ファイルも送付します。
また、この問題に対する正しい解き方が別にあるのでしょうか。
ソフトに直接関係ない話も多く混ざってしまい大変恐縮ではありますが、
お時間の余裕のある時で構いませんので、お返事を下さると助かります。
ここまでお読み下さり、ありがとうございました。
以下の問題のグラフを描きたいと思っていますが、上手く書けませんでした。
当たりくじ赤が出る確率は常にaで一定、
当たりくじ青が出る確率は常にbで一定、
ハズレくじが出る確率は常に(1-a-b)で一定、
今は、a=bであると仮定します。
この条件下で、くじをn回引いたとき、
少なくとも５回以上当たりくじ赤が出て、かつ、少なくとも５回以上当たりくじ青が出る確率Pn(10≦n)を、
nの値に応じて確率が変化する様子をグラフで描く
という問題を考えています。
(これよりもさらに複雑な条件の問題を考えていますが、まずはこの問題が解けないとどうしようもないので。)
以下、自分が考えた解法です。
(赤が出る回数が0回、青が出る回数が0～n回いずれかになる確率)=A0
(赤が出る回数が1回、青が出る回数が0～n-1回いずれかになる確率)=A1
(赤が出る回数が2回、青が出る回数が0～n-2回いずれかになる確率)=A2
(赤が出る回数が3回、青が出る回数が0～n-3回いずれかになる確率)=A3
(赤が出る回数が4回、青が出る回数が0～n-4回いずれかになる確率)=A4
A=A0+A1+A2+A3+A4、と定義
(赤が出る回数が0～n回いずれか、青が出る回数が0回になる確率)=B0
(赤が出る回数が0～n-1回いずれか、青が出る回数が1回になる確率)=B1
(赤が出る回数が0～n-2回いずれか、青が出る回数が2回になる確率)=B2
(赤が出る回数が0～n-3回いずれか、青が出る回数が3回になる確率)=B3
(赤が出る回数が0～n-4回いずれか、青が出る回数が4回になる確率)=B4
B=B0+B1+B2+B3+B4、と定義
(赤が出る回数が0回、青が出る回数が0～4回いずれかになる確率)=C0
(赤が出る回数が1回、青が出る回数が0～4回いずれかになる確率)=C1
(赤が出る回数が2回、青が出る回数が0～4回いずれかになる確率)=C2
(赤が出る回数が3回、青が出る回数が0～4回いずれかになる確率)=C3
(赤が出る回数が4回、青が出る回数が0～4回いずれかになる確率)=C4
C=C0+C1+C2+C3+C4、と定義
ここで、a=bより、A=Bであるから
求める確率Pnは、
Pn=1-(A+B)+C
=1-2A+C
になると思ったので、AとCを計算しようと思い
まずは確率C=C0+C1+C2+C3+C4を計算しようと思いました。
ソフトでの表記方法に従うと、例えばC3の場合、
C3=(n,Sum(t,0,4,n!/3!t!(n-t-3)!×a^3×b^t×(1-a-b)^(n-t-3))
だと思ったので、
Cの場合だと、
C=(n,Sum(s,0,4,Sum(t,0,4,n!/s!t!(n-s-t)!×a^s×b^t×(1-a-b)^(n-s-t)))
次にAは
A=Sum(u,0,4,a^u×(1-a)^(n-u)×nCr(n,u))
になると思いました。
ここで、Pn=1-2A+C
のPnをグラフを描こうと思い、
パラメータを例えば、a=b=0.02の場合と仮定して、これをグラフにしたところ、
かなり早い段階でグラフが途切れてしまいました。
pdfでの説明の通りに、(変域の上端ー下端)/増減幅≦5000の範囲にしてるのですが、なぜこんなに早くグラフが途切れるのでしょうか。
この問題では、どう入力するのが正しかったのでしょうか。ファイルも送付します。
また、この問題に対する正しい解き方が別にあるのでしょうか。
ソフトに直接関係ない話も多く混ざってしまい大変恐縮ではありますが、
お時間の余裕のある時で構いませんので、お返事を下さると助かります。
ここまでお読み下さり、ありがとうございました。
[添付]: 4896 bytes
Re: 7/16に質問をした者です
考え方の問題ではなく，GRAPESの計算限界によるものです。
また，それを回避する方法もります。
サンプルも添付します。
計算限界というのは「n!」です。
948! までは計算できますが，949! 以上は桁数のオーバーフローで計算できなくなります。
そこで，
n! /s!t!(n-s-t)! を nCr(n,s)* nCr(n-s,t)
と変形することで，オーバーフローを回避しました。
数学的には，
n! /s!t!(n-s-t)! ＝ nCr(n,s)* nCr(n-s,t)
ですが，GRAPES内部では
nCr(n,s) = n/s * (n-1)/(s-1) * ・・・* (n-s+1)/1
という計算をしているので，オーバーフローを回避できるのです。
また，それを回避する方法もります。
サンプルも添付します。
計算限界というのは「n!」です。
948! までは計算できますが，949! 以上は桁数のオーバーフローで計算できなくなります。
そこで，
n! /s!t!(n-s-t)! を nCr(n,s)* nCr(n-s,t)
と変形することで，オーバーフローを回避しました。
数学的には，
n! /s!t!(n-s-t)! ＝ nCr(n,s)* nCr(n-s,t)
ですが，GRAPES内部では
nCr(n,s) = n/s * (n-1)/(s-1) * ・・・* (n-s+1)/1
という計算をしているので，オーバーフローを回避できるのです。
[添付]: 5270 bytes
Re: 7/16に質問をした者です
A 
2018/07/22(Sun) 00:12 No.2477
なるほど、よく理解できました。
これでようやく、安心して本題を解き始めることができます。
お返事ありがとうございました。
これでようやく、安心して本題を解き始めることができます。
お返事ありがとうございました。
A 2018/07/22(Sun) 00:12 No.2477
シグマを含むグラフについて
関係式の欄での、シグマを含むグラフについての質問です。
y=Sum(k,1,x,k)と入力してグラフを描こうとしたところ、
y=0の定数関数に似たグラフになってしまいました。
(実際には、X軸の右端から赤の直線が伸びてる点が異なります)
y=x(x+1)/2
のようなグラフを書こうとしたのですが、
その場合はどのようにシグマを用いて入力すれば良かったのでしょうか。
実際にはやや複雑な式のグラフを書こうとしていたためシグマを用いる必要性があったのですが、
上記のような単純な関係式で躓いてしまったため、今回の質問することに決めた次第です。
宜しければ、ご返答をお願い致します。
y=Sum(k,1,x,k)と入力してグラフを描こうとしたところ、
y=0の定数関数に似たグラフになってしまいました。
(実際には、X軸の右端から赤の直線が伸びてる点が異なります)
y=x(x+1)/2
のようなグラフを書こうとしたのですが、
その場合はどのようにシグマを用いて入力すれば良かったのでしょうか。
実際にはやや複雑な式のグラフを書こうとしていたためシグマを用いる必要性があったのですが、
上記のような単純な関係式で躓いてしまったため、今回の質問することに決めた次第です。
宜しければ、ご返答をお願い致します。
Re: シグマを含むグラフについて
ともだ 2018/07/16(Mon) 21:01 No.2465
関数や関係式の中で，シグマ，Π，定積分の変域にｘを入れることはできません。
ご指摘のようなグラフを描く場合には，媒介変数表示の曲線や点列を使います。
例えば
P = ( n , Sum(k,1,n,k)) 0 <= n <= 10
とします。
サンプルを添付します。
ご指摘のようなグラフを描く場合には，媒介変数表示の曲線や点列を使います。
例えば
P = ( n , Sum(k,1,n,k)) 0 <= n <= 10
とします。
サンプルを添付します。
[添付]: 4796 bytes
ともだ 2018/07/16(Mon) 21:01 No.2465
Re: シグマを含むグラフについて
A 2018/07/16(Mon) 23:38 No.2466
今の簡単な式については理解しました。
それとは別に、自分が解いている問題があるのですが、
この方法を使っても上手くグラフを描けませんでした。
もう何日か粘ってみて分からない場合は、また質問に来ます。
お返事、どうもありがとうございました。
それとは別に、自分が解いている問題があるのですが、
この方法を使っても上手くグラフを描けませんでした。
もう何日か粘ってみて分からない場合は、また質問に来ます。
お返事、どうもありがとうございました。
A 2018/07/16(Mon) 23:38 No.2466
GRAPES講習会について
今年は開催の予定はありますでしょうか。
もし予定されていれば，日程などはいつ頃公開されますでしょうか。
もし予定されていれば，日程などはいつ頃公開されますでしょうか。
Re: GRAPES講習会について
申し訳ありませんが，GRAPES講習会は昨年で最終回とさせていただいています。
現在，iOS版の開発が進んでいますので，形を変えて実施することもあるかもしれませんが，今年度の予定はありません。
現在，iOS版の開発が進んでいますので，形を変えて実施することもあるかもしれませんが，今年度の予定はありません。
Re: GRAPES講習会について
tanak 2018/07/06(Fri) 21:29 No.2463
今まで，色々と勉強をさせて頂いてきて，今年もと思っていたので残念です。
別の機会があればぜひ参加させて頂きます。
ありがとうございました。
別の機会があればぜひ参加させて頂きます。
ありがとうございました。
tanak 2018/07/06(Fri) 21:29 No.2463
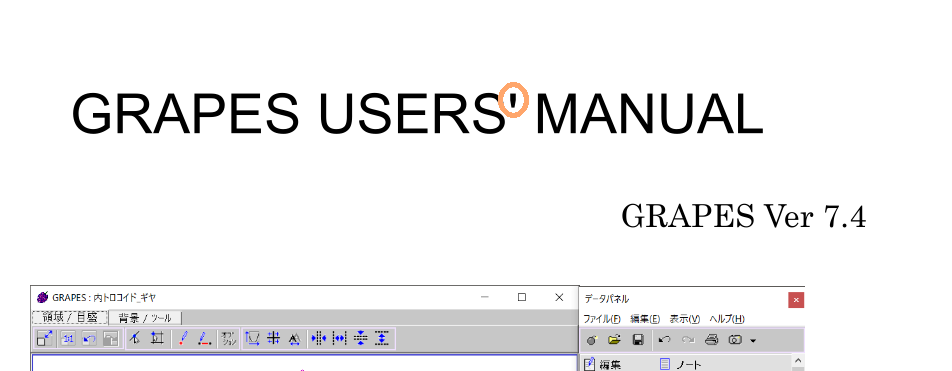
GRAPES 7.40のPDFマニュアル1ページ目にタイポがあります
こんにちは。
GRAPES 7.40のPDFマニュアル1ページ目にタイポがありました(画像のようになっており、アポストロフィの位置が違います。7.18や6.91のPDFマニュアルは正しくなっておりました)。
これは余談なのですが、私がGRAPESを使っているOSはWindows 2000のSP4で、6.83では動作していたのですが、それ以降のバージョンでは起動しなくなっておりました。それが、この7.40では起動して使えるようになっております。
開発に使ってらっしゃるDelphiのバージョンなどが関係しているのかもしれません。
(7.40と7.18はXPでも起動して使えるようです。7.18と6.91は自分の環境のWindows 2000では起動せず、「プロシージャエントリポイント GetSystemTimes がダイナミックリンクライブラリ kernel32.dllから見つかりませんでした」というエラーダイアログが表示されて起動しません。「起動するようにしてほしい」などといった要望ではなくて、単なる報告です)
GRAPES 7.40のPDFマニュアル1ページ目にタイポがありました(画像のようになっており、アポストロフィの位置が違います。7.18や6.91のPDFマニュアルは正しくなっておりました)。
これは余談なのですが、私がGRAPESを使っているOSはWindows 2000のSP4で、6.83では動作していたのですが、それ以降のバージョンでは起動しなくなっておりました。それが、この7.40では起動して使えるようになっております。
開発に使ってらっしゃるDelphiのバージョンなどが関係しているのかもしれません。
(7.40と7.18はXPでも起動して使えるようです。7.18と6.91は自分の環境のWindows 2000では起動せず、「プロシージャエントリポイント GetSystemTimes がダイナミックリンクライブラリ kernel32.dllから見つかりませんでした」というエラーダイアログが表示されて起動しません。「起動するようにしてほしい」などといった要望ではなくて、単なる報告です)
Re: GRAPES 7.40のPDFマニュアル1ページ目にタイポがあります
ともだ 2018/06/16(Sat) 15:13 No.2459
USER'S と USERS' の違いですが，
後者の方は 「ユーザー達の」という意味になります。
ですので，後者の方が正解かと思っています。
win2000との相性については，全く分かりません。
報告ありがとうございました。
後者の方は 「ユーザー達の」という意味になります。
ですので，後者の方が正解かと思っています。
win2000との相性については，全く分かりません。
報告ありがとうございました。
ともだ 2018/06/16(Sat) 15:13 No.2459
Re: GRAPES 7.40のPDFマニュアル1ページ目にタイポがあります
亀ライフ 2018/06/16(Sat) 16:18 No.2460
お返事ありがとうございます。
アポストロフィを後ろにつける用法があるのですね。知らなかったので勉強になりました。
アポストロフィを後ろにつける用法があるのですね。知らなかったので勉強になりました。
亀ライフ 2018/06/16(Sat) 16:18 No.2460
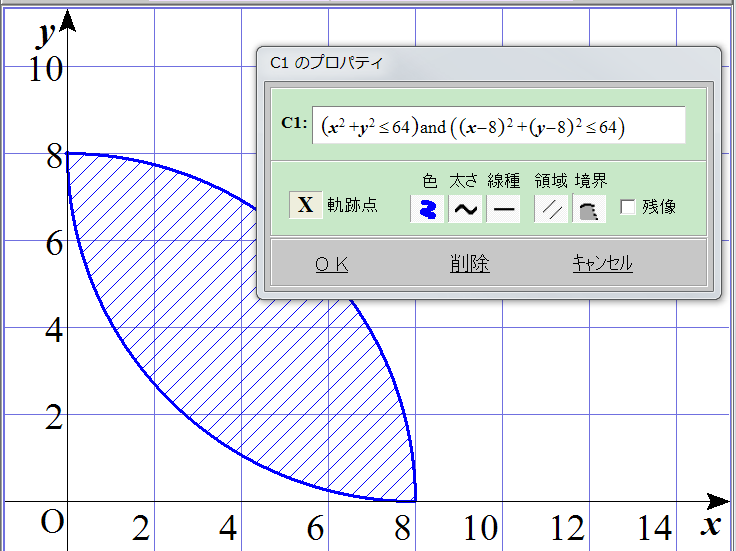
領域に綺麗に色を塗りたい
お世話になります。
正方形の中に四分円を描き、重なったところに色を塗りたいのですが、
(0,0)と(8,8)を対角線とする正方形に
x^2+y^2<=64 and (x-8)^2+(y-8)^2<=64
と入力したところ、添付画像のように色が塗られる部分が荒く、端まで綺麗に塗られません。
色々試行錯誤しましたが解決せず……
どのようにすれば良いでしょうか。
正方形の中に四分円を描き、重なったところに色を塗りたいのですが、
(0,0)と(8,8)を対角線とする正方形に
x^2+y^2<=64 and (x-8)^2+(y-8)^2<=64
と入力したところ、添付画像のように色が塗られる部分が荒く、端まで綺麗に塗られません。
色々試行錯誤しましたが解決せず……
どのようにすれば良いでしょうか。
Re: 領域に綺麗に色を塗りたい
ともだ 2018/05/20(Sun) 16:15 No.2425
共通部分を表示するには，それぞれの式をカッコでくくって，and で結びます。
(x^2+y^2<=64) and ((x-8)^2+(y-8)^2<=64)
PDFマニュアルの「4-3 複数の領域の共通部分と和集合」を参照してください。
(x^2+y^2<=64) and ((x-8)^2+(y-8)^2<=64)
PDFマニュアルの「4-3 複数の領域の共通部分と和集合」を参照してください。
ともだ 2018/05/20(Sun) 16:15 No.2425
Re: 領域に綺麗に色を塗りたい
mk 2018/05/20(Sun) 19:00 No.2426
ご回答ありがとうございます。
カッコがあると斜線などで表示されるのはわかっていたのですが、できれば色を塗りたいのです。
色々試行錯誤しているうちにカッコをつけないと色が塗られるということを発見し、このような質問をした次第です。
色を塗るのはGRAPESではできないという認識で宜しいでしょうか。
カッコがあると斜線などで表示されるのはわかっていたのですが、できれば色を塗りたいのです。
色々試行錯誤しているうちにカッコをつけないと色が塗られるということを発見し、このような質問をした次第です。
色を塗るのはGRAPESではできないという認識で宜しいでしょうか。
mk 2018/05/20(Sun) 19:00 No.2426
Re: 領域に綺麗に色を塗りたい
ともだ 2018/05/20(Sun) 20:08 No.2427
ご指摘の通り「関係式（陰関数）」ではべた塗りはできません。
ただ，「曲線」を使えばできます。
ただ，「曲線」を使えばできます。
ともだ 2018/05/20(Sun) 20:08 No.2427
Re: 領域に綺麗に色を塗りたい
mk 2018/05/20(Sun) 21:11 No.2428
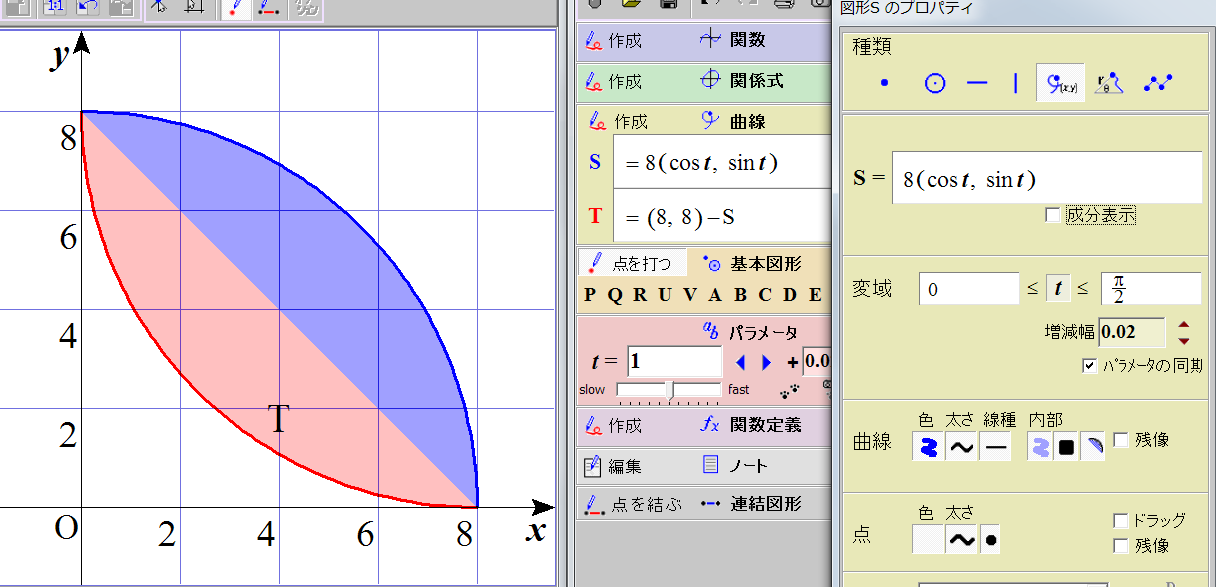
そのような方法があったのですね。
勉強不足でした。
お手数おかけいたしました。ありがとうございました。
勉強不足でした。
お手数おかけいたしました。ありがとうございました。
mk 2018/05/20(Sun) 21:11 No.2428
微分
高校生です。
数Ⅲの課題でxを無限大に飛ばした時の関数のグラフを書いたのですが、ほんとかなと思ってGRAPESを使ってやろうとおもいました。
しかし、limとか∞とかわからなくてグラフをかけませんでした。
どのように動作したらよいでしょうか…
数Ⅲの課題でxを無限大に飛ばした時の関数のグラフを書いたのですが、ほんとかなと思ってGRAPESを使ってやろうとおもいました。
しかし、limとか∞とかわからなくてグラフをかけませんでした。
どのように動作したらよいでしょうか…
Re: 微分
ともだ 2018/05/12(Sat) 23:05 No.2420
無限大のときの値を正直に計算することはGRAPESにはできません。
しかし，t = 1/x と置き換えれば，
lim(x→∞,f(x)) = lim(t→+0 ,f(1/t))
ですから，y=f(1/x) のグラフをかいて，y軸との切片を観察すれば極限を知ることができるのではないでしょうか。
もしかして，x→∞ ではなくて，n→∞ ですか？
それなら，nをどんどん大きくしていけば，極限の様子を知ることができます。
しかし，t = 1/x と置き換えれば，
lim(x→∞,f(x)) = lim(t→+0 ,f(1/t))
ですから，y=f(1/x) のグラフをかいて，y軸との切片を観察すれば極限を知ることができるのではないでしょうか。
もしかして，x→∞ ではなくて，n→∞ ですか？
それなら，nをどんどん大きくしていけば，極限の様子を知ることができます。
ともだ 2018/05/12(Sat) 23:05 No.2420
ウィキペディアに投稿
お世話になります。
ウィキペディアに「T-expression」というタイトルで投稿いたしました。2018年３月１０日アップ。
グレイプスを使って工夫して描いた図柄を紹介しております。
お時間があれば、是非ご覧くださいませ。
T-expression です。
ウィキペディアに「T-expression」というタイトルで投稿いたしました。2018年３月１０日アップ。
グレイプスを使って工夫して描いた図柄を紹介しております。
お時間があれば、是非ご覧くださいませ。
T-expression です。
Re: ウィキペディアに投稿
ともだ 2018/04/11(Wed) 22:21 No.2412
拝見しました。
とてもきれいなグラフィックで驚きました，
もう，十分芸術ですね，
とてもきれいなグラフィックで驚きました，
もう，十分芸術ですね，
ともだ 2018/04/11(Wed) 22:21 No.2412
Re: ウィキペディアに投稿
ある中学校でグレイプスソフトをダウンロードさせて、
T-expressionの描き方を指導してきました。
ところが、既存のPCが廃棄されて今年から iPad が40台ほど設置されたそうで、この夏の指導をどうしようか、と思案しているところです。グレイプスをiPad でもダウンロードして同じかたちで操作できますでしょうか。
T-expressionの描き方を指導してきました。
ところが、既存のPCが廃棄されて今年から iPad が40台ほど設置されたそうで、この夏の指導をどうしようか、と思案しているところです。グレイプスをiPad でもダウンロードして同じかたちで操作できますでしょうか。
Re: ウィキペディアに投稿
ともだ 2018/05/06(Sun) 23:02 No.2417
現状では,GRAPESはwindowsでしか動きません。
iPAD版あるいはhtml版の開発も徐々に進んでいますが，夏に間に合うかどうかは微妙です。
また，スクリプトなどの高度な機能までサポートするのは難しいと思います。
iPAD版あるいはhtml版の開発も徐々に進んでいますが，夏に間に合うかどうかは微妙です。
また，スクリプトなどの高度な機能までサポートするのは難しいと思います。
ともだ 2018/05/06(Sun) 23:02 No.2417
Re: ウィキペディアに投稿
ご返事賜りありがとうございます。
今後ともご指導のほどよろしくお願いいたします。
ありがとうございました。
今後ともご指導のほどよろしくお願いいたします。
ありがとうございました。