巨大化してしまう
いつもお世話になっています。
作成した図をWordに貼り付けるとき、なぜか巨大なサイズになってしまいます。
倍率を見ても、その巨大化している状態で100%となっています。
縮小で対処しているので特に問題はないのですが、いつからそうなってしまったかも覚えていません。
設定の問題？
Wordの年式やOSの問題？
バグ？
何が原因かわからないので、モヤモヤします。
もしご存じでしたら教えていただけると助かります。
作成した図をWordに貼り付けるとき、なぜか巨大なサイズになってしまいます。
倍率を見ても、その巨大化している状態で100%となっています。
縮小で対処しているので特に問題はないのですが、いつからそうなってしまったかも覚えていません。
設定の問題？
Wordの年式やOSの問題？
バグ？
何が原因かわからないので、モヤモヤします。
もしご存じでしたら教えていただけると助かります。
mk
Re: 巨大化してしまう
ともだ 
2019/11/04(Mon) 15:40 No.2578
精密なイメージを作るには，大きなキャンパスが要ります。
データ解像度を上げれてピクセルを小さくすればキャンパスは小さくて済むのですが，解像度を上げていくと，なぜか画面の端が切れたり偏ったりしてしまうのです。
メタファイル形式で描画していて，これの理解が足りないからでしょうけど，原因がつかめません。
というわけで，いまの仕様がWORD等に貼り付けたときに不具合いを生じないギリギリの線なのです。
なお，以前はデータ解像度を犠牲にしていました。イラストレータなどに取り込んで拡大していくと，ギザギザが見えてきます。
データ解像度を上げれてピクセルを小さくすればキャンパスは小さくて済むのですが，解像度を上げていくと，なぜか画面の端が切れたり偏ったりしてしまうのです。
メタファイル形式で描画していて，これの理解が足りないからでしょうけど，原因がつかめません。
というわけで，いまの仕様がWORD等に貼り付けたときに不具合いを生じないギリギリの線なのです。
なお，以前はデータ解像度を犠牲にしていました。イラストレータなどに取り込んで拡大していくと，ギザギザが見えてきます。
ともだ 2019/11/04(Mon) 15:40 No.2578
Re: 巨大化してしまう
mk 2019/11/04(Mon) 17:26 No.2579
ご回答ありがとうございます。
「せっかく小さなサイズで作ったのに，巨大化したら意味ないじゃん！」
という身勝手な考えでしたが、やむを得ないのですね。
図の作成に支障があるわけではないので、このまま使わせていただきます。
お手数おかけしました。
ありがとうございました。
「せっかく小さなサイズで作ったのに，巨大化したら意味ないじゃん！」
という身勝手な考えでしたが、やむを得ないのですね。
図の作成に支障があるわけではないので、このまま使わせていただきます。
お手数おかけしました。
ありがとうございました。
mk 2019/11/04(Mon) 17:26 No.2579
終了できません
すばらしいソフトに感激・感謝しております．最新版をインストールしました．grapesを閉じようとすると，「control palette の設定に失敗しました」との表示が出て，後は堂々巡りになってしまい困っています．以前はこんなことなかったのですが．
Re: 終了できません
何らかのバグです。
たまに起こるようですが，今のところ原因不明ですが，もう一度調べなおしてみます。
たまに起こるようですが，今のところ原因不明ですが，もう一度調べなおしてみます。
解決しました
ご多忙のところ恐縮です．先ほどの「終了できません」の件ですが，解決しました．インストールの際，最初の操作で，「保存」でなく「開く」をタップしていたことが原因でした．初歩的なミスでお手を煩わせました．
Re: 終了できません
> 「保存」でなく「開く」をタップしていたことが原因
よかったです。
でも，そのような操作と「control paltte ・・・」というメッセージの関係が気になりますが・・・
よかったです。
でも，そのような操作と「control paltte ・・・」というメッセージの関係が気になりますが・・・
Re: 終了できません
全く同じ状況で困っています。
追記されていたように自分も保存できていなかったのかもしれない、保存しなおしましたが状況は変わらず…。
具体的にどうされて解決なされましたか？
追記されていたように自分も保存できていなかったのかもしれない、保存しなおしましたが状況は変わらず…。
具体的にどうされて解決なされましたか？
ポスターなどに拡大
お世話になります。
Grapes活用のGraphic artが大分広がりつつあります。
例えば、A1版の拡大ポスターに、グレイプス上の画面程度の
quality を確保しながら印刷できる方法があればお教えいただきたいのですが。
50inchのTV画面で拡大しても、見た目のqualityは確保できるものですか。
数年後には「理数」の表現知識・技能が求められてくるようです。
Grapes活用のGraphic artが大分広がりつつあります。
例えば、A1版の拡大ポスターに、グレイプス上の画面程度の
quality を確保しながら印刷できる方法があればお教えいただきたいのですが。
50inchのTV画面で拡大しても、見た目のqualityは確保できるものですか。
数年後には「理数」の表現知識・技能が求められてくるようです。
無題
全く同じ状況で困っています。
追記されていたように自分も保存できていなかったのかもしれない、保存しなおしましたが状況は変わらず…。
具体的にどうされて解決なされましたか？
追記されていたように自分も保存できていなかったのかもしれない、保存しなおしましたが状況は変わらず…。
具体的にどうされて解決なされましたか？
単純にお礼
モンゴルの大学で日本留学試験対策および留学後の工学授業向けに日本語での数学授業を担当しております。
赴日前の学生のブラッシュアップに更に面白い数学授業をと彷徨いGRAPESにたどり着きました。
本当に素晴らしいソフトにめぐり合えたように思います。
これから他の先生方の実践教案なども含め勉強させていただきご報告できるような活動にしていけるよう頑張ります。
お礼のような決意表明 いや、自分を追い込むために。
（＾～＾）
赴日前の学生のブラッシュアップに更に面白い数学授業をと彷徨いGRAPESにたどり着きました。
本当に素晴らしいソフトにめぐり合えたように思います。
これから他の先生方の実践教案なども含め勉強させていただきご報告できるような活動にしていけるよう頑張ります。
お礼のような決意表明 いや、自分を追い込むために。
（＾～＾）
格子線の色と点線の粗さ
こんばんは。お世話になっています。
以前ステッカーのずれについて書き込んだ者です。
7.60をDLして試してみましたが、画面端はどうしても多少ずれてしまうようですね。
今回はそれとは別に2点、質問があります。
1.
格子線が必要な図を作成するとき、格子線の色が薄いため、
プリンタで印刷→コピー機で印刷をすると、格子線が消えてしまいます。
そのため、格子線を黒にしたいのですが、格子線の色を変える方法はあるのでしょうか？
また、変えられないとしたら、機能として追加することは可能でしょうか？
2.
格子線や連結図形などで点線を選ぶと、かなり目が細かい点線で描かれますが、
プリンタで印刷→コピー機で印刷をすると、点線が潰れて直線のようになってしまいます。
もっと点線を粗くする、もしくは点線の粗さを選択できるようにすることはできないでしょうか？
お忙しいとは思いますが、ご回答いただけると幸いです。
以前ステッカーのずれについて書き込んだ者です。
7.60をDLして試してみましたが、画面端はどうしても多少ずれてしまうようですね。
今回はそれとは別に2点、質問があります。
1.
格子線が必要な図を作成するとき、格子線の色が薄いため、
プリンタで印刷→コピー機で印刷をすると、格子線が消えてしまいます。
そのため、格子線を黒にしたいのですが、格子線の色を変える方法はあるのでしょうか？
また、変えられないとしたら、機能として追加することは可能でしょうか？
2.
格子線や連結図形などで点線を選ぶと、かなり目が細かい点線で描かれますが、
プリンタで印刷→コピー機で印刷をすると、点線が潰れて直線のようになってしまいます。
もっと点線を粗くする、もしくは点線の粗さを選択できるようにすることはできないでしょうか？
お忙しいとは思いますが、ご回答いただけると幸いです。
Re: 格子線の色と点線の粗さ
ともだ 2019/09/09(Mon) 11:49 No.2568
ステッカーの位置については，印刷用と画面表示用では解像度が違うので，どうしても少しのずれが生じます。
正確な位置が必要で，かつ1行しか表示しないのであれば，点のラベルで代用してみてください。
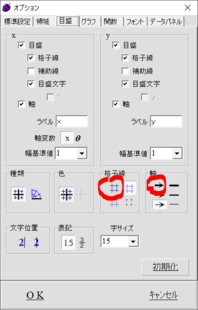
格子線については，色を濃くすることができます。
目盛オプションで，選ぶことができます。
また，軸を太くすると目盛格子線も太くなります。
今の仕様では，点線の細かさは固定です。Office図形との互換性を持たせるためには，これを変更することはできないと考えています。
点線の細かさは線の太さに比例するので，線を太くすれば，少しはましになるのではないでしょうか。
正確な位置が必要で，かつ1行しか表示しないのであれば，点のラベルで代用してみてください。
格子線については，色を濃くすることができます。
目盛オプションで，選ぶことができます。
また，軸を太くすると目盛格子線も太くなります。
今の仕様では，点線の細かさは固定です。Office図形との互換性を持たせるためには，これを変更することはできないと考えています。
点線の細かさは線の太さに比例するので，線を太くすれば，少しはましになるのではないでしょうか。
ともだ 2019/09/09(Mon) 11:49 No.2568
Re: 格子線の色と点線の粗さ
mk 2019/09/09(Mon) 13:37 No.2569
ご回答ありがとうございます。
ステッカーは任意に座標の数字を入れたいときなどに使うだけなので、
特別困るというほどではありません。
格子線については、色を濃くできるのは以前から気付いていましたが、
それでも黒になるわけではなく、コピー機で印刷すると消えてしまうのです。
できるのであれば、もっと濃い、できれば真っ黒の格子線が描けるようになったらいいな、と思います。
点線は仕方ないのですね。
太いと主張が激しくなってしまうので、ちょっとそれは……
ただ、Wordなどで図形の線種を点線にすると、潰れることなく点線で印刷されますし、点線の粗さも全然違うように見えます。
私はgrapesで図やグラフを作成した後、
画面コピー→Wordなどに図を張り付け
で図を挿入していますが、これが原因なのでしょうか？
ステッカーは任意に座標の数字を入れたいときなどに使うだけなので、
特別困るというほどではありません。
格子線については、色を濃くできるのは以前から気付いていましたが、
それでも黒になるわけではなく、コピー機で印刷すると消えてしまうのです。
できるのであれば、もっと濃い、できれば真っ黒の格子線が描けるようになったらいいな、と思います。
点線は仕方ないのですね。
太いと主張が激しくなってしまうので、ちょっとそれは……
ただ、Wordなどで図形の線種を点線にすると、潰れることなく点線で印刷されますし、点線の粗さも全然違うように見えます。
私はgrapesで図やグラフを作成した後、
画面コピー→Wordなどに図を張り付け
で図を挿入していますが、これが原因なのでしょうか？
mk 2019/09/09(Mon) 13:37 No.2569
Re: 格子線の色と点線の粗さ
ともだ 2019/09/10(Tue) 15:03 No.2570
印刷時の軸や目盛の濃さについては，検討してみます。
なお，GRAPESで書いたグラフをコピーしてWORDに貼り付けた場合の線の太さは，
１．線の太さはGRAPESグラフ画面の大きさに関わらず一定で，目盛オプションの軸の太さで決まります。
つまり，大きな画面で作ったグラフは，小さな画面で作ったグラフより，相対的に線が細くなります。
２．WORDに貼り付けた後，拡大縮小すると，線の幅も伸縮します。
線の幅を変えずに伸縮する方法として，WORD図形に変換する方法もあります（図形を右クリックして「図の編集」）が，いろいろと手間がかかります。
幅1000Pixelsのグラフ画面上に幅２Pixelの軸を描いたときと，幅500pixelsの画面上に同じ幅の軸を描いたときでは，WORD上では後者の方が２倍太く印刷されます。（目盛格子線は軸の2/3倍，補助線は1/2倍の太さで印刷されます。）
WORD上で縮小される場合には，それを見込んで軸を太めにしておく必要があります。
参考になりましたでしょうか。
なお，GRAPESで書いたグラフをコピーしてWORDに貼り付けた場合の線の太さは，
１．線の太さはGRAPESグラフ画面の大きさに関わらず一定で，目盛オプションの軸の太さで決まります。
つまり，大きな画面で作ったグラフは，小さな画面で作ったグラフより，相対的に線が細くなります。
２．WORDに貼り付けた後，拡大縮小すると，線の幅も伸縮します。
線の幅を変えずに伸縮する方法として，WORD図形に変換する方法もあります（図形を右クリックして「図の編集」）が，いろいろと手間がかかります。
幅1000Pixelsのグラフ画面上に幅２Pixelの軸を描いたときと，幅500pixelsの画面上に同じ幅の軸を描いたときでは，WORD上では後者の方が２倍太く印刷されます。（目盛格子線は軸の2/3倍，補助線は1/2倍の太さで印刷されます。）
WORD上で縮小される場合には，それを見込んで軸を太めにしておく必要があります。
参考になりましたでしょうか。
ともだ 2019/09/10(Tue) 15:03 No.2570
Re: 格子線の色と点線の粗さ
mk 2019/09/11(Wed) 02:25 No.2571
ご丁寧な回答ありがとうございます。
格子線の色については気長に待ちます。
線については詳しく教えていただきましたが……
仕組みを知らないままソフトを使わせていただいていますので、正直わからない部分もあります。
基本的に拡大縮小はせずにサイズ100%で貼り付けていますが、いろいろ試してみたいと思います。
お手数おかけしました。
ありがとうございました。
格子線の色については気長に待ちます。
線については詳しく教えていただきましたが……
仕組みを知らないままソフトを使わせていただいていますので、正直わからない部分もあります。
基本的に拡大縮小はせずにサイズ100%で貼り付けていますが、いろいろ試してみたいと思います。
お手数おかけしました。
ありがとうございました。
mk 2019/09/11(Wed) 02:25 No.2571
直線の記号表示について
3D-GRAPESについてお聞きしたいことがあります。
添付ファイルの直線ABをlと記号表示したいのですが，画面中央あたりに表示されます。
これを画面の端の方に表示させることは可能でしょうか。
よろしくお願いします。
添付ファイルの直線ABをlと記号表示したいのですが，画面中央あたりに表示されます。
これを画面の端の方に表示させることは可能でしょうか。
よろしくお願いします。
[添付]: 3809 bytes
Re: 直線の記号表示について
ともだ 2019/09/06(Fri) 21:26 No.2565
たしかに，直線と半直線については，ラベル表示位置がはっきりしません。見直す余地はありそうです。
ただ，画面端というのは結構難しいのです。画面の奥に３次元的に存在している直線について，視野の端っこの点・・・。しかも，無限遠点を考慮する必要がある。ちょっと無理っぽいような・・・
ただ，画面端というのは結構難しいのです。画面の奥に３次元的に存在している直線について，視野の端っこの点・・・。しかも，無限遠点を考慮する必要がある。ちょっと無理っぽいような・・・
ともだ 2019/09/06(Fri) 21:26 No.2565
Re: 直線の記号表示について
tanak 2019/09/08(Sun) 22:00 No.2566
ご回答ありがとうございます。
別の方法で説明することを考えます。
別の方法で説明することを考えます。
tanak 2019/09/08(Sun) 22:00 No.2566
縮小して縮小して・・・
お世話になります。
周期関数を使って、例えば、sin(x^2+y^2)=t としてt を変化させて無数の円を描きます。画面を縮小して、さらに縮小して進めていくと、干渉縞が現れてきます。大変美しいのです。その状態を越えてさらに縮小を続けていくと、ある時を期して突然拡大されたような映像が顕れます。
これは、何を観ているのでしょうか。お教えいただけたら嬉しいです。
周期関数を使って、例えば、sin(x^2+y^2)=t としてt を変化させて無数の円を描きます。画面を縮小して、さらに縮小して進めていくと、干渉縞が現れてきます。大変美しいのです。その状態を越えてさらに縮小を続けていくと、ある時を期して突然拡大されたような映像が顕れます。
これは、何を観ているのでしょうか。お教えいただけたら嬉しいです。
Re: 縮小して縮小して・・・
ともだ 2019/08/17(Sat) 13:49 No.2558
画面はピクセルで構成されています。
例えば，画面が1000x1000のピクセルで構成されているとしましょう。
そうすると，画面にはあなたが描いたたくさんの円と，縦横1000本ずつの細い線が描かれているように見えます。
同心円の幅が広いうちは何も見えませんが，狭くなってくると，縦横の線と干渉を起こし，モアレが生じます。
画像は，同心円と平行線によるモアレです。ご指摘のものは，これにさらに横線が加わったものと考えられます。
例えば，画面が1000x1000のピクセルで構成されているとしましょう。
そうすると，画面にはあなたが描いたたくさんの円と，縦横1000本ずつの細い線が描かれているように見えます。
同心円の幅が広いうちは何も見えませんが，狭くなってくると，縦横の線と干渉を起こし，モアレが生じます。
画像は，同心円と平行線によるモアレです。ご指摘のものは，これにさらに横線が加わったものと考えられます。
ともだ 2019/08/17(Sat) 13:49 No.2558
Re: 縮小して縮小して・・・
モアレは薄いカーテンなどでよく見受けられますが、
これ、干渉縞の模様からもう少し研究してみます。
ありがとうございました。
これ、干渉縞の模様からもう少し研究してみます。
ありがとうございました。
Re: 縮小して縮小して・・・
モアレについて検討してみました。
むしろ、モアレ等を理数的に解析できる方法だということが分かってきました。
本ソフトウェアのもう一つの活用法が見つかりました。
ありがとうございます。
むしろ、モアレ等を理数的に解析できる方法だということが分かってきました。
本ソフトウェアのもう一つの活用法が見つかりました。
ありがとうございます。
フラクタル図形が描けません
GRAPESでフラクタルの図形を描きたいと思っているのですが、下記の参照URLをもとに描こうとすると無効なスクリプト名「call(fractal,X,z,0)」などが表示されます。どう対処すればよろしいでしょうか。
Re: フラクタル図形が描けません
ともだ 2019/08/17(Sat) 14:03 No.2559
この質問は，私ではなく，このレポートの執筆者にすべきです。
が，若干の補足を行ったgpsファイルを添付します。
スクリプトに変更は加えていません。
もしｋして，空行が消えてしまっていませんか？
が，若干の補足を行ったgpsファイルを添付します。
スクリプトに変更は加えていません。
もしｋして，空行が消えてしまっていませんか？
[添付]: 6460 bytes
ともだ 2019/08/17(Sat) 14:03 No.2559
ノートのステッカーがずれる
こんばんは。
お忙しいとは思いますが、質問させていただきます。
ノートのステッカーで、後で必要になった文字などを追加すると、
既に入力・配置済みのステッカーがずれて表示されてしまうのです。
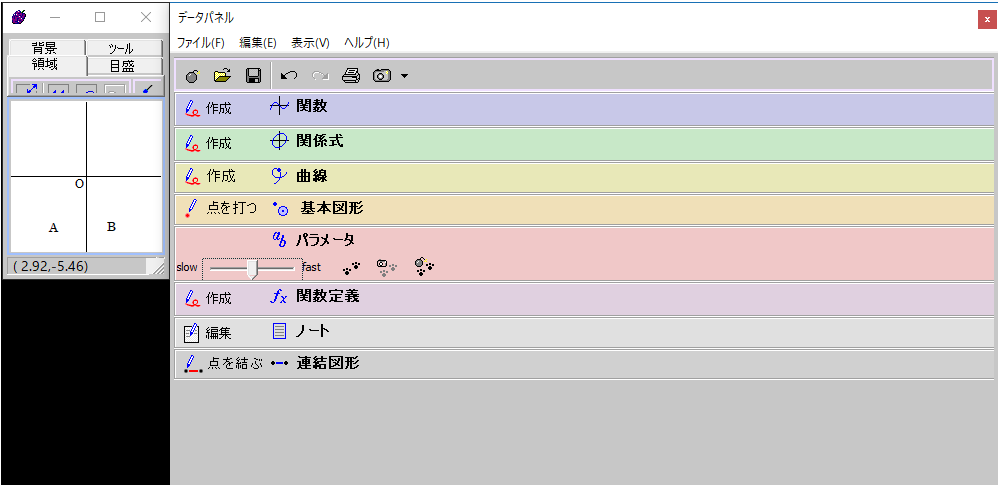
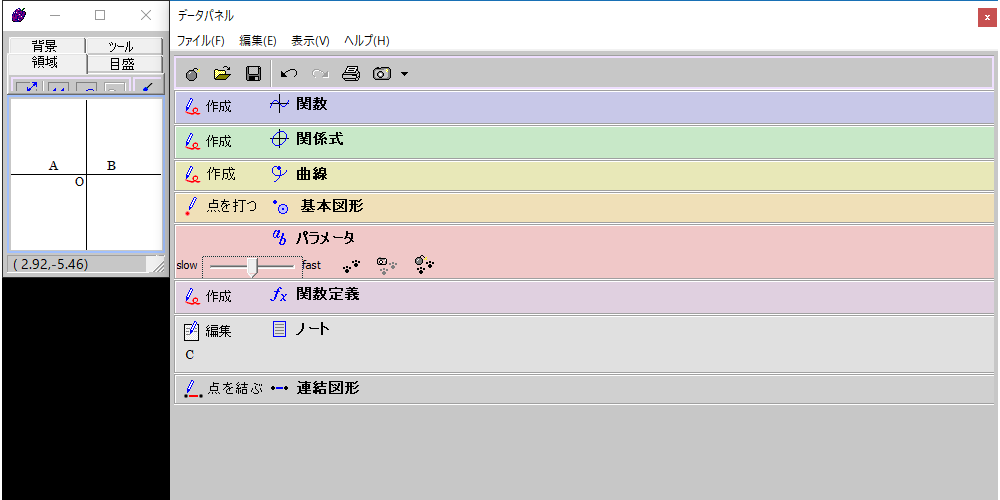
このように、AとBをステッカーとして配置し、
その後にノートのステッカーで「C」と追加すると……
お忙しいとは思いますが、質問させていただきます。
ノートのステッカーで、後で必要になった文字などを追加すると、
既に入力・配置済みのステッカーがずれて表示されてしまうのです。
このように、AとBをステッカーとして配置し、
その後にノートのステッカーで「C」と追加すると……
Re: ノートのステッカーがずれる
mk 2019/07/14(Sun) 00:00 No.2547
このように、配置済みのAやBがずれてしまうのです。
仕様でしょうか？バグでしょうか？
それとも、私の使い方がおかしいからでしょうか？
仕様でしょうか？バグでしょうか？
それとも、私の使い方がおかしいからでしょうか？
mk 2019/07/14(Sun) 00:00 No.2547
Re: ノートのステッカーがずれる
ステッカーの位置が，グラフ画面の下方80ピクセルあたりより下に差し掛かるとき，再配置してしまうようです。
修正します。
修正します。
Re: ノートのステッカーがずれる
mk 2019/07/14(Sun) 01:33 No.2549
ご回答ありがとうございます。
そして素早いご対応ありがとうございます。
宜しくお願いします。
そして素早いご対応ありがとうございます。
宜しくお願いします。
mk 2019/07/14(Sun) 01:33 No.2549