楕円の定義
2定点F,Gからの距離の和が一定であるような点の軌跡を楕円という。つまり,楕円上の点をPとすると,
PF+PG=一定が成り立つ。
右図では。2つの同心円群の重なるところを順に結んでいくと楕円が得られる。
これをグラフィックデザイン風にしたのが,数学教育09年3月号の表紙である。
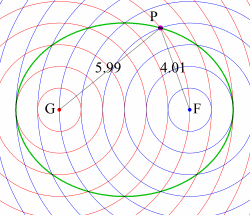
楕円(PF+PG=一定)
楕円の接線の性質
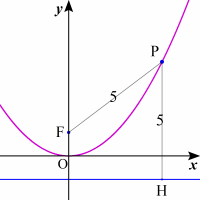
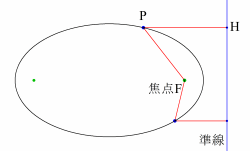
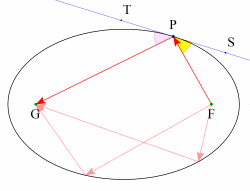
楕円の定義における2点F,Gを楕円の焦点という。楕円上の点Pにおける接線SPTを引くと,
∠FPS=∠GPTが成り立つ。これの幾何による証明は,意外とと簡単で中学生でも理解できるのではないだろうか。
証明は,「2次曲線ランド-資料館-楕円-接線」にあるので,ぜひご覧いただきたい。
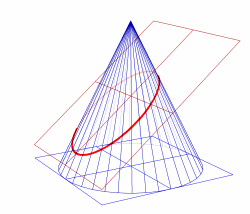
このことから,鏡でできた楕円形の部屋があるとき,一方の焦点に光源を置くと,壁に当たった光は反射して,もう一方の焦点に向かう。このように,楕円の焦点には,放物線と同様に,光を集める性質がある。
楕円の焦点と接線
楕円の部屋を反射する光
ここまでは,よく知られたことである。では,楕円形の鏡の部屋で,焦点以外の点から出発した光は,どのような軌跡を描いていくのだろうか?
右図はその例のひとつだが,「Visual壁新聞 - 楕円を反射する光」に資料があるので,これもぜひご覧いただきたい。
大変美しい性質である。
これも,やや複雑ではあるが,幾何の知識で証明できる。