2008年12月号の補足

１　定積分と区分求積法
２　定積分の近似計算
３　GRAPESと積分
４　データファイルのDownload

１．定積分と区分求積法

　区分求積法では，
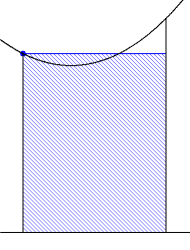
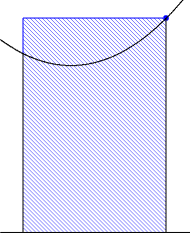
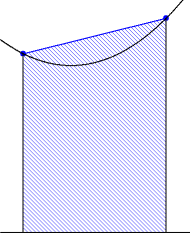
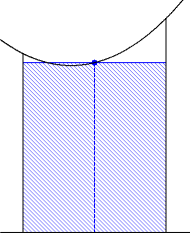
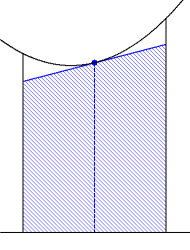
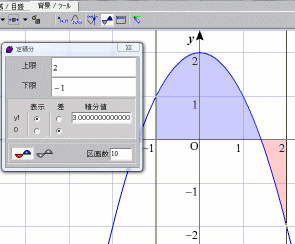
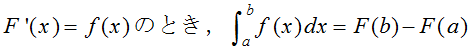  1. 積分区間を細分する。
  2. 各区間では関数は定数であるとみなして，（関数値×個々の区間の幅）を求める。
  3. ２で求めた値を，すべての区間について加える。
の手順で，積分の近似値を求める。そして，さらに，
１〜３について，区間の細分をどこまでも細かくしていった時の極限を求める。
というプロセスで，積分値を計算することができる。この方法はリーマン積分と呼ばれ，定積分の定義の標準的なものである。
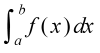　という積分の記号は，この考え方に由来する。「dx」は無限に細分された区間を表しており，「f(x)dx」は無限に細い長方形の面積を表している。そして，∫は，f(x)dx を集めてくるという意味である。よく知られているように，∫は和を表すSumの頭文字「S」に由来している。

積分と微分の間には，逆演算の関係が成り立つ。すなわち，
である。これは微積分の基本定理と呼ばれている。この定理があるおかげで，区分求積法による面倒な計算を経ることなく積分の値を求めることができる。

　現在の高校の教科書では，これを逆手にとって，上記の等式を定積分の定義としている。つまり，積分とは何かということを教えないままに，積分と微分は逆演算であることを教えているのである。結果，高校生にとって，積分とは微分の逆演算でしかなく，積分記号の中の dx が何を意味するのかさえ彼らは知らない。論理的につじつまが合っていればよいという考えもあるが，このような理解では，数学以外の分野（物理，経済など）に利用することができない。
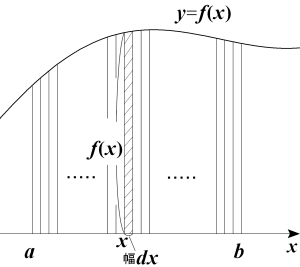
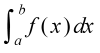のイメージ

２．定積分の近似計算（区分求積法とシンプソンの公式）

　微分の計算は，高校程度で出てくる関数であれば，必ずできるが，積分の計算は簡単ではない。ちょうど，式の展開と因数分解みたいなものだと言えなくもない。そこで，定積分の値を近似的に求めることが必要になってくる。ここでは，区分求積法とシンプソンの公式について述べる。

左端区分求積法

　区分求積法において，各区間の関数値をその区間の左端の関数値で代表させる方法である。

右端区分求積法

　区分求積法において，各区間の関数値をその区間の右端の関数値で代表させる方法である。

台形近似法

　区分求積法では各区間を長方形で近似しているのに対し，台形近似法では台形で近似する。言い換えれば，左端近似や右端近似では関数を定数とみなしているのに対し，台形近似では１次式で近似していることになる。が，いずれにしても凹凸のある関数には対応できない。なお，台形近似は，左端近似と右端近似の値の平均になっている。

中点法

　各区間の関数値をその区間の中点の関数値で代表させる方法である。
　定数近似であるにもかかわらず，１次近似の台形近似と同じくらい正確なのが不思議である。これは，中点におけるグラフの接線を用いた台形近似と同じ値を持つことから納得できる。

シンプソン法

　２次関数の積分について，この台形近似法と中点法で求めたときの誤差を調べると，
　　（台形近似法での誤差）：（中点法での誤差）＝ ２：（−１）
になっている。ここで，台形近似法による値をA，中点法による値をBとすると，A＋２Bを計算すれば，誤差が消えることに気がつく。このようにして，新しい近似公式　（A＋２B）／３ を得る。実は，これがシンプソンの公式である。
左端区分求積法
右端区分求積法
台形近似法

中点法
中点法
台形法と中点法の違い

３．GRAPESと積分

GRAPESでは，定積分を扱うことができる。

定積分window

これを使うと，積分区間と積分値をグラフで見ることができる。
定積分ボタンをクリックして，定積分windowを表示すると，積分区間と積分値が表示される。値が正の部分は青で，負の部分は赤で表示されている。
積分区間を示す垂直のバーは，マウスのドラッグで移動することができる。また，定積分window内の「上限」「下限」の欄をクリックして，関数電卓からの入力で積分区間を変更することもできる。

定積分の計算

これとは別に，式の中で定積分を扱うことができる。
∫(x , a , b , f(x) )
とすれば，x=a から x=b までの定積分を求めることができる。
GRAPESはノンインテリジェントなシステムなので，積分を理論的に計算するなどということはできない。しかし，近似的に計算することはできて，９次までの多項式の積分であれば，誤差なく計算することができる。
参照：定積分の高次近似式
図のクリックで拡大

４．データファイルのDownload