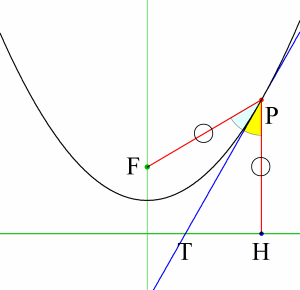
ひとつ目は,放物線の基本性質で,放物線には焦点と準線があり,放物線上の任意の点Pから焦点Fを結んだ線分PFの長さと,点Pから準線に引いた垂線PHの長さは等しい。すなわち,
PF = PH実は,これは放物線の図形的な定義である。
二つ目は接線で,これについてもきれいな性質がある。
点Pにおける接線をPTとすると,PTは∠FPHを二等分する。すなわち,
∠FPT = ∠HPTが成り立つ。上記の2つの性質はパラボラアンテナの原理にもなっている。
このあたりの性質の関しては,ここを参照されたい。
1 放物線の接線
2 放物線の接線の方程式
3 1次近似,2次近似,・・・
4 データファイルのDownload
| 本文中では,「放物線の接線は,グラフを拡大しないと引けない」,つまり,微分の考え方抜きには接線を引くことができない,と書いているが,もちろん,これは正確ではない。ただ,円の接線の性質が図形の対称性から簡単に得られることに比べると,放物線の接線の性質を導くのはけっこう難しい。ここでは,放物線の基本的な性質(定義)と,接線の性質を紹介する。 ひとつ目は,放物線の基本性質で,放物線には焦点と準線があり,放物線上の任意の点Pから焦点Fを結んだ線分PFの長さと,点Pから準線に引いた垂線PHの長さは等しい。すなわち, PF = PH実は,これは放物線の図形的な定義である。 二つ目は接線で,これについてもきれいな性質がある。 点Pにおける接線をPTとすると,PTは∠FPHを二等分する。すなわち, ∠FPT = ∠HPTが成り立つ。上記の2つの性質はパラボラアンテナの原理にもなっている。 このあたりの性質の関しては,ここを参照されたい。 |
 |
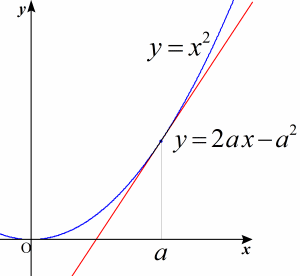
放物線C:y = x2 の接線が 直線L:y = 2ax - a2 であることを求めるには,微分や判別式といった高校数学の知識が必要になるが,直線Lが放物線Cの接線になっていることを示すだけなら,比較的簡単にできる。y = x2 と y = 2ax - a2 の y座標の差を計算すると, x2 - ( 2ax - a2) = ( x - a )2 ≧ 0 (等号成立は,x = a のときのみ)であるから,x = a では放物線Cと直線Lは重なり,それ以外では放物線Cの方が直線Lより上方にあることがわかる。 このことは,放物線 y = x2 の x = a における接線は, y = 2ax - a2であることを示している。 |
 |
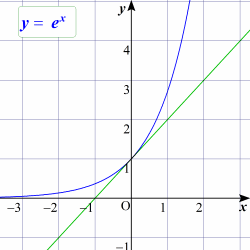
| 微分の本質は,関数を極微の世界で眺めた時の1次近似である。関数のグラフを,グラフ上の任意の点( p , q ) を中心にどこまでも拡大していくと,直線に見えてくる。その時の直線,すなわち1次関数を,関数の
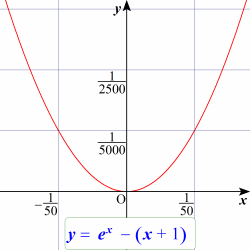
x = p における1次近似式という。 では,元の関数式と1次近似の近似式との差はどのようになるのだろうか。指数関数を例に確かめてみよう。 y = ex の x = 0 での接線の傾きは 1 なので,接線の方程式は,y = x + 1 である。そこで, y = ex - (x + 1)のグラフを描いてみると,2次関数のグラフに似ている。とくに原点付近を拡大すると,もうほとんど2次関数 y = (1/2) x2 である。つまり, ex - (x + 1) ≒ (1/2) x2こうして, y = ex の2次近似式 ex ≒ (1/2) x2 + x + 1を得る。 では, y = ex - { (1/2) x2 + x + 1 }のグラフを描くとどうなるのか? 実はこの話はどこまでも続く。(それが Taylor展開だということにそろそろお気づきだと思う) |
 |
 |