 |
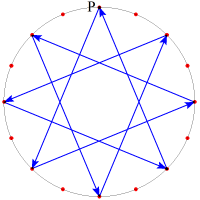 |
| (n,a)=(16,6)の途中図 | (n,a)=(16,6)の完成図 |
1 星形正多角形と約数・倍数の関係
2 分数正多角形
3.データファイルのDownload
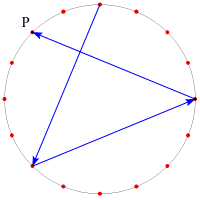
正n角形の頂点のひとつの位置に点Pがあり,これをa個ずつ進めていく。
点Pの止まった跡を結んでいくと星形正多角形ができるが,nとaによって,どのような星形ができるかを考えてみよう。
(n,a)=(16,6)の途中図 (n,a)=(16,6)の完成図
点Pをx回進めてちょうど星形が完成したとする。このとき,点Pは最初の位置に戻っているから,
ax=kn
が成り立つ。ここでkは整数であり,点Pが最初の位置に戻るまでに円周を何周するかを表している。
上図の例では,点Pは
8回進んだときに最初の位置に戻り,
この間に円周を3周するから,
x=8,k=3 である。
このとき,6・8=3・16 である。
ax=kn=L とおくと,Lはnとaの最小公倍数であるから,
x=L/a , k=L/n (Lはnとaの最小公倍数)
が成り立つ。
ここで,2数n,aの最大公約数をGと表せば,LG=na
であるから,
x=n/G , k=a/G (Gはnとaの最大公約数)
が成り立つ。
とくに,nとaが互いに素であるとき,G=1
であるから,x=n が成り立つ。
これは逆も成り立つから,
「点Pがすべての頂点を通る条件は,nとaが互いに素であること」
である。
nとaが2以上の公約数を持つとき,nとaの最大公約数をGとし,n=n’G,a=a’G とすれば,
(n,a)=(15,6)
x=5,k=2(n,a)=(5,2)
x=5,k=2xとkで形が決まる。
a’x=kn’が成り立つことから,
(n,a)の2数が作る星形と(n’,a’)の2数が作る星形は同じである。
簡単に表現すれば,
例えば,数学教育12月号本文P79上部の五芒星では,
(n,a)=(10 , 4),(15 , 6),(20 , 8),(25 , 10) であり,
これらはいずれも,(n,a)=(5 , 2)と同じ形である。
2数n,aが与えられたとき,これらを「約分」しても星形は変わらない。
そこで,(n,a)が作る星形をn/a角形(a分のn角形)と表現することがある。
a=1 のとき,n/a=nであり,また図形も正n角形になることから,この表現は,正n角形という表現方法の拡張になっている。
五芒星は5/2角形(2分の5角形)である。
注:n/a角形という場合,(n,a)が作る星形と(n,n−a)が作る星形は同形であるから,a<n/2 とするのが普通である。